In his highly-recommended book Information dashboard design, data-presentation guru Stephen Few criticises pie charts as being a poor way to present numerical data and I quite strongly agree. Although they seem to be a good way to compare relative quantities, they have real limitations especially when there are more than about five categories to compare. A horizontal bar chart is nearly always going to be a better choice because

1. there is always space to put a label against each item;
2. you can accommodate more categories;
3. relative values are easier to judge;
4. you can rank entries for greater clarity;
5. it will take less space while being more legible; and
6. you don’t need to rely on colour coding (meaning colours can be used to emphasise particular items if needed).

Pie charts with numerous categories and a colour-coded key can be incredibly difficult to interpret, even for readers with perfect colour perception, and bad luck if you ever have to distribute black-and-white photocopies of them.

Data presentation is one of the topics I cover in my advanced M&T master classes. For forthcoming dates click here

ONE OF MY GREAT FRUSTRATIONS when training people in the analysis and presentation of energy consumption data is that there are very few commercial software products that do the job sufficiently well to deserve recommendation. If any developers out there are interested, these are some of the things you’re typically getting wrong:

1. Passive cusum charts: energy M&T software usually includes cusum charting because it is widely recognised as a desirable feature. The majority of products, however, fail to exploit cusum’s potential as a diagnostic aid, and treat it as nothing more than a passive reporting tool. What could you do better? The key thing is to let the user interactively select segments of the cusum history for analysis. This allows them, for example, to pick periods of sustained favourable performance in order to set ‘tough but achievable’ performance targets; or to diagnose behaviour during abnormal periods. Being able to identify the timing, magnitude and nature of an adverse change in performance as part of a desktop analysis is a powerful facility that good M&T software should provide.

2. Dumb exception criteria: if your M&T software flags exceptions based on a global percentage threshold, it is underpowered in two respects. For one thing the cost of a given percentage deviation crucially depends on the size of the underlying consumption and the unit price of the commodity in question. Too many users are seeing a clutter of alerts about what are actually trivial overspends.

Secondly, different percentages are appropriate in different cases. Fixed-percentage thresholds are weak because they are arbitrary: set the limit too low, and you clutter your exception reports with alerts which are in reality just normal random variations. Set the threshold too high, and solvable problems slip unchallenged under the radar. The answer is to set a separate threshold individually for each consumption stream. It sounds like a lot of work, but it isn’t; it should be be easy to build the required statistical analysis into the software.

3. Precedent-based targets: just comparing current consumption with past periods is a weak method. Not only is it based on the false premise that prevailing conditions will have been the same; if the users happens to suffer an incident that wastes energy, it creates a licence to do the same a year later. There are fundamentally better ways to compute comparison values, based on known relationships between consumption and relevant driving factors.

Tip: if your software does not treat degree-day figures, production statistics etc as equal to consumption data in importance, you have a fundamental problem

4. Showing you everything: sometimes the reporting philosophy seems to be “we’ve collected all this data so we’d better prove it”, and the software makes no attempt to filter or prioritise the information it handles. A few simple rules are worth following.

1. Your first line of defence can be a weekly exception report (daily if you are super-keen);
2. The exception report should prioritise incidents by the cost of the deviations from expected consumption;
3. It should filter out or de-emphasise those that fall within their customary bounds of variability;
4. Only in significant and exceptional cases should it be necessary to examine detailed records.

5. Bells and whistles: presumably in order to give salesmen something to wow prospective customers, M&T software commonly employs gratuitous animation, 3-D effects, superfluous colour and tricksy elements like speedometer dials. Ridiculously cluttered ‘dashboards’ are the order of the day.

Tip: please, please read Stephen Few’s book “Information dashboard design”

Current details of my courses and masterclasses on monitoring and targeting can be found here

Background: conventional energy monitoring

In classic monitoring and targeting practice, consumption is logged at regular intervals along with relevant associated driving factors and a formula is derived which computes expected consumption from those factors. A common example would be expected fuel consumption for space heating, calculated from measured local degree-day values via a simple straight-line relationship whereby expected consumption equals a certain fixed amount per week plus so many kWh per degree-day. Using this simple mathematical model, weekly actual consumptions can then be judged against expected values to reveal divergence from efficient operation regardless of weather variations. The same principle applies in energy-intensive manufacturing, external lighting, air compressors, vehicles and any other situation where variation in consumption is driven by variation in one or more independently measurable factors. The expected-consumption models may be simple or complex.

Comparing actual and expected consumptions through time gives us valuable graphical views such as control charts and cusum charts. These of course rely on the data being sequential, i.e., in the correct chronological sequence, but they do not necessarily need the data to be consecutive. That is to say, it is permissible to have gaps, for instance to skip invalid or missing measurements.

The Brigadoon method

“Brigadoon” is a 1940s Broadway musical about a mythical Highland village that appears in the real world for only one day a year (although as far as its inhabitants are concerned time is continuous) and its plot concerns two tourists who happen upon this remote spot on the day that the village is there. The story came to mind some years ago when I was struggling to deal with energy monitoring of student residences. Weekly fuel consumption naturally dropped during vacations (or should do) and I realised I would need two different expected-consumption models, one for occupied weeks and another for unoccupied weeks using degree-days computed to a lower base temperature. One way to accommodate this was to have a single more complex model that took the term/vacation state into account. In the event I opted for splitting the data history into two: one for term weeks, and the other for vacation weeks. Each history thus had very long gaps in it, but there is no objection to closing up the gaps so that in effect the last week of each term is immediately followed by the first week of the next and likewise for vacations.

This strategy made the single building into two different ones. Somewhat like Brigadoon, the ‘vacant’ manifestation of the building for instance only comes into existence outside term time, but it appears to have a continuous history. The diagram below shows the control chart using a single degree-day model on the left, as per conventional practice, while on the right we see the separate control charts for the two virtual buildings, plotted with the same limits to show the reduction in modelling error.

Not just space heating

This principle can be used in many situations. I have used it very successfully on distillation columns in a chemical works to eliminate non-steady-state operation. I recommended it for a dairy processing plant with automatic meter reading where the night shift only does cleaning while the day shift does production: the meters can be read at shift change to give separate ‘active’ and ‘cleaning’ histories for every week. A friend recently asked me to look at data collected from a number of kilns with batch firing times extending over days, processing different products; here it will be possible to split the histories by firing programme: one history for programme 20, another for 13, and so on.

When monitoring consumption in outside lighting circuits with photocell control, it is reasonable to expect weekly consumption to vary according to how many hours of darkness there were. And that’s exactly what we can see here in this Spanish car park:

It is a textbook example: with the exception of two weeks, it shows the tighest correlation that I have ever seen in any energy-consuming system.

The negative intercept is interesting, and a glance at the daily demand profile (viewed as a heatmap) shows how it comes about:

Moving left to right we see from January to March the duration of daylight (zero consumption in blue) increases. High consumption starts at dusk and finishes at dawn, but from about 10 p.m. to 5 a.m. it drops back to a low level. It is this “missing” consumption for about seven hours in the night which creates the negative intercept. If they kept all the lights on from dusk to dawn the line would go through the origin.

For weekly and monthly tabulations of hours of darkness (suitable for England and other countries on similar latitudes)  click here.

I began monitoring this external lighting circuit at a retail park in the autumn of 2016. It seems from the scatter diagram below that it exhibits weekly consumption which is well-correlated with changing daylight availability expressed as effective hours of darkness per week.

The only anomaly is the implied negative intercept, which I will return to later; when you view actual against expected consumption, as below, the relationship seems perfectly rational:

Consumption follows the annual sinusoidal profile that you might expect.

But what about that negative intercept? The model appears to predict close to zero consumption in the summer weeks, when there would still be roughly six hours a night of darkness. One explanation could be that the lights are actually habitually turned off in the middle of the night for six hours when there is no activity. That is entirely plausible, and it is a regime that does apply in some places, but not here. For evidence see the ‘heatmap’ view of half-hourly consumption from September to mid November:

As you can see, lighting is only off during hours of daylight; note by the way how the duration of daylight gradually diminishes as winter draws on. But the other very clear feature is the difference before and after 26 October when the overnight power level abruptly increased. When I questioned that change, the explanation was rather simple: they had turned on the Christmas lights (you can even see they tested them mid-morning as well on the day of the turn-on).

So that means we must disregard that week and subsequent ones when setting our target for basic external lighting consumption. This puts a different complexion on our regression analysis. If we use only the first four weeks’ data we get the relationship shown with a red line:

In this modified version, the negative intercept is much less marked and the data-points at the top right-hand end of the scatter are anomalous because they include Christmas lighting. There are, in effect, two behaviours here.

The critical lesson we must draw is that regression analysis is just a statistical guess at what is happening: you must moderate the analysis by taking into account any engineering insights that you may have about the case you are analysing

Just to illustrate why building energy performance indicators can’t really be expected to work. Here we have four buildings with identical volumes and floor areas (same set of Lego blocks) but just look at the different amount of external wall, roof and ground-floor perimeter – even exposed soffit in two of them.

But all is not lost: there are techniques we can use to benchmark dissimilar buildings, in some cases leveraging submeters and automatic meter reading, but also using good old-fashioned whole-building weekly manual meter readings if that’s all we have. Join me for my lunchtime lecture on 23 February to find out more

The traditional way to compare buildings’ fuel consumptions is to use annual kWh per square metre. When they are in the same city, evaluated over the same interval, and just being compared with each other, there is no need for any normalisation. So it was with “Office S” and “Office T” which I recently evaluated. I found that Office S uses 65 kWh per square metre and Office T nearly double that. Part of the difference is that Office T is an older building; and it is open all day Saturday and Sunday morning, not just five days a week. But desktop analysis of consumption patterns showed that Office T also has considerable scope to reduce its demand through improved control settings.

Two techniques were used for the comparison. The first is to look at the relationship between weekly gas consumption and the weather (expressed as heating degree days).

The chart on the right shows the characteristic for Office S. Although not a perfect correlation, it exhibits a rational relationship.

Office T, by contrast, has a quite anomalous relationship which actually looked like two different behaviours, one high one during the heating season and another in milder weather.

The difference in the way the two heating systems behave can be seen by examining their half-hourly consumption patterns. These are shown below using ‘heat map’ visualisations for the period 3 September to 10 November, i.e., spanning the transition from summer to winter weather. In an energy heatmap each vertical stripe is one day, midnight to midnight GMT from top to bottom and each cell represents half an hour. First Office S. You can see its daytime load progressively becoming heavier as the heating season progresses:

Compare Office T, below. It has some low background consumption (for hot water) but note how, after its heating system is brought into service at about 09:00 on 3 October, it abruptly starts using fuel at similar levels every day:

Office T displays classic signs of mild-weather overheating, symptomatic of faulty heating control. It was no surprise to find that its heating system uses radiators with weather compensation and no local thermostatic control. In all likelihood the compensation slope has been set too shallow – a common and easily-rectified failing.

By the way, although it does not represent major energy waste, note how the hot water system evidently comes on at 3 in the morning and runs until after midnight seven days a week.

This case history showcases two of the advanced benchmarking techniques that will be covered in my lunchtime lecture in Birmingham on 23 February 2017 (click here for more details).

In energy-intensive manufacturing processes there is a need to benchmark production units against each other and against yardstick figures. Conventional wisdom has it that you should compare specific energy ratios (SER), of which kWh per gross tonne is one common example. It seems simple and obvious but, as anybody will know who has tried it, it does not really work because a simple SER varies with output, and this clouds the picture.

To illustrate the problem and to suggest a solution, this article picks some of the highlights from a pilot exercise to benchmark air compressors. These are the perfect thing for the purpose not least because they are universally used and obey fairly straightforward physical laws. Furthermore, because they are all making a similar product from the same raw material, they should in principle be highly comparable with each other.

Various conventions are used for expressing compressors’ SERs but I will use kWh per cubic metre of free air. From the literature on the subject you might expect a given compressor’s SER to fall in the range 0.09 to 0.14 kWh/m³ (typically). Lower SER values are taken to represent better performance.

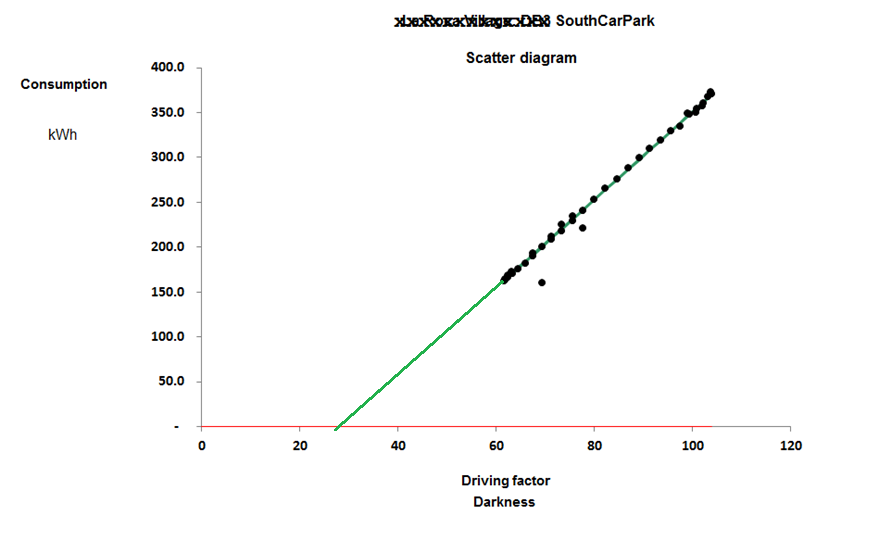
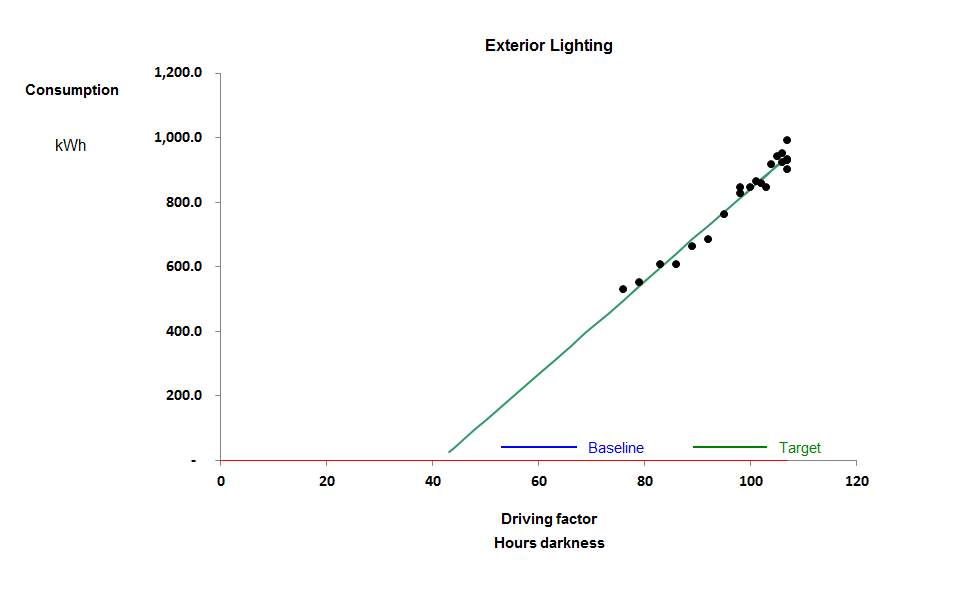
The drawback of the SER approach is that some compressor installations, like any energy-intensive process, have a certain fixed standing load independent of output. The compressor installation in Figure 1 has a standing load of 161 kWh per day for example, and this has a distorting effect: if you divide kWh by output at an output of 9,000 m³ you should find the SER is just under 0.12 kWh/m³ but at a low daily output, say 4,000 m³ , you get 0.14 kWh/m³. The fixed consumption makes performance look more variable than it really is and changes in throughput change the SER whereas in reality, with a small number of obvious exceptions, the performance of this particular compressor looks quite consistent.

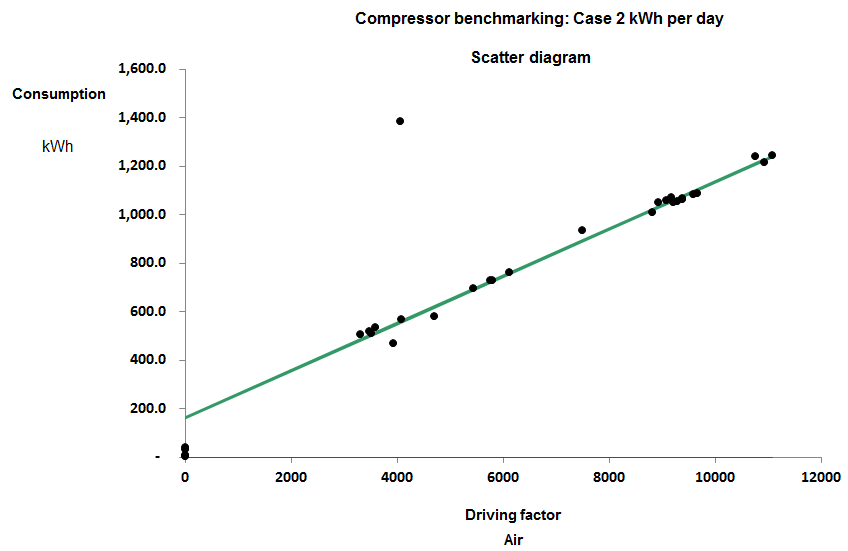
Figure 1

When I say it looks consistent I mean that consumption has a consistent straight-line relationship with output. The gradient of the best-fit straight line does not change across the normal operating range: it is said to be a ‘parameter’. In parametric benchmarking we compare compressors’ marginal SERs, that is, the gradients of their energy-versus-output scatter diagrams. The other parameter that we might be interested in is the standing load, i.e., where the diagonal characteristic crosses the vertical (kWh) axis.

The compressor installation in Figure 1 is one of eight that I compared in a pilot study whose results were as follows:

============================
Case   Marginal  Standing 
No     SER       kWh per day
----------------------------
 8      0.085       115 
 5      0.090        62 
 1      0.092     3,062 
 2      0.097       161 
 7      0.105        58 
 6      0.124        79 
 3      0.161       698 
============================

As you can see, the marginal SERs are mainly fairly comparable and may prove to be more so once we have taken proper account of inlet temperatures and delivery pressures. But their standing kWh per day are wildly different. It makes little sense to try comparing the standing loads. In part they are a function of the scale of the installation (Case 1 is huge) but also the metering may be such that unrelated constant-ish loads are contributing to the total. The variation in energy with variation in output is the key comparator.

In order to conduct this kind of analysis, one needs frequent meter readings, and the installations in the pilot study were analysed using either daily or weekly figures (although some participants provided minute-by-minute records). Rich data like this can be filtered using cusum analysis to identify inconsistencies, so for example in Case 3, although there is no space to go into the specific here, we found that performance tended to change dramatically from time to time and the marginal SER quoted in the table is the best that was consistently achieved.

Case 7 was found to toggle between two different characteristics depending on its loading: see Figure 2. At higher outputs its marginal SER rose to 0.134 kWh/m³, reflecting the relatively worse performance of the compressors brought into service to match higher loads.

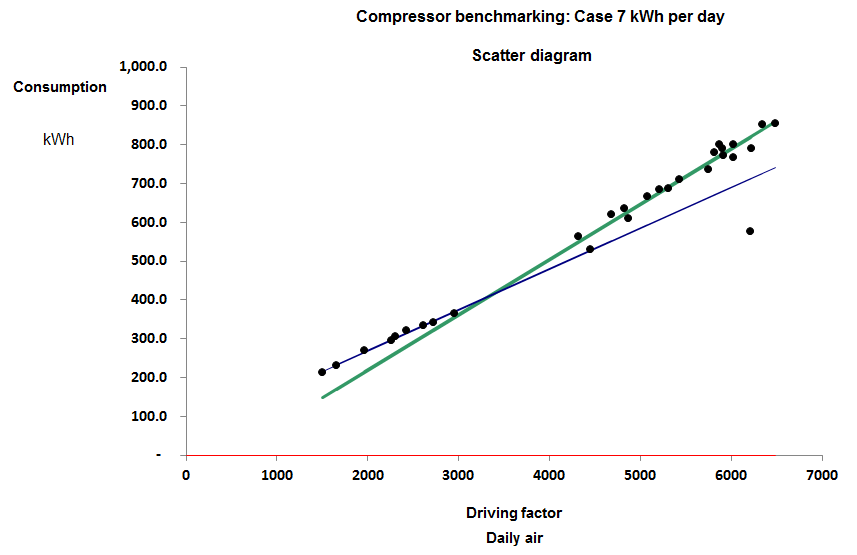
Figure 2

In Case 8, meanwhile, the compressor plant changed performance abruptly at the start of June, 2016. Figure 3 compares performance in May with that on working days in June and we obtained the following explanation. The plant consists of three compressors. No.1 is a 37 kW variable-speed machine which takes the lead while Nos 2 and 3 are identical fixed-speed machines also of 37 kW rating. Normally, No.2 takes the load when demand is high but during June they had to use No.3 instead and the result was a fixed additional consumption of 130 kWh per day. The only plausible explanation is that No. 3 leaks 63 m³ per day before the meter, quite possibly internally because of defective seals or non-return vales. Enquiries with the owner revealed that they had indeed been skimping on maintenance and they have now had a quote to have the machines overhauled with an efficiency guarantee.

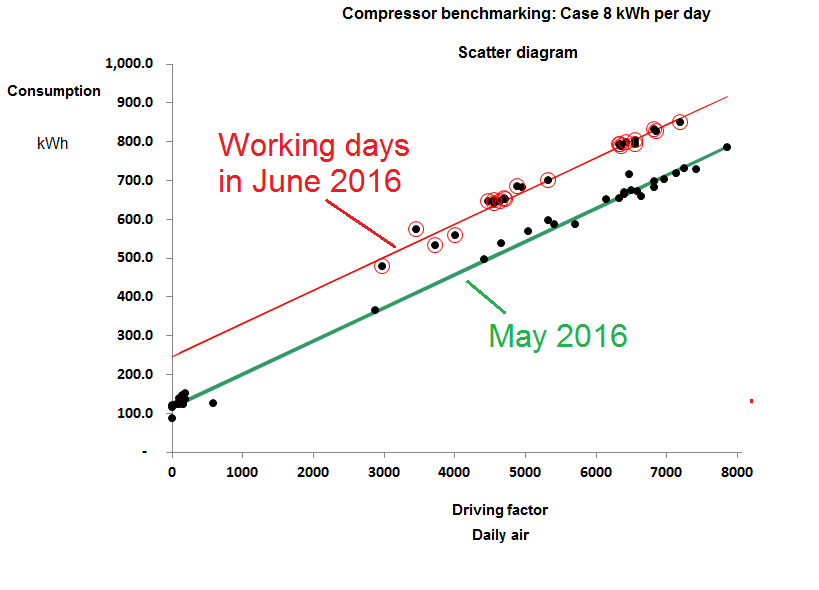Figure 3

This last case is one of three where we found variations in performance through time on a given installation and were able to isolate the period of best performance. It improves a benchmarking exercise if one can focus on best achievable, rather than average, performance; this is impossible with the traditional SER approach, as is the elimination of rogue data. Nearly all the pilot cases were found to include clear outliers which would have contaminated a simple SER.

Deliberately excluding fixed overhead consumption from the analysis has two significant benefits:

• It enables us to compare installations of vastly differing sizes, and
• it means we can tolerate unrelated equipment sharing the meter as long as its contribution to demand is reasonably constant.