I began monitoring this external lighting circuit at a retail park in the autumn of 2016. It seems from the scatter diagram below that it exhibits weekly consumption which is well-correlated with changing daylight availability expressed as effective hours of darkness per week.

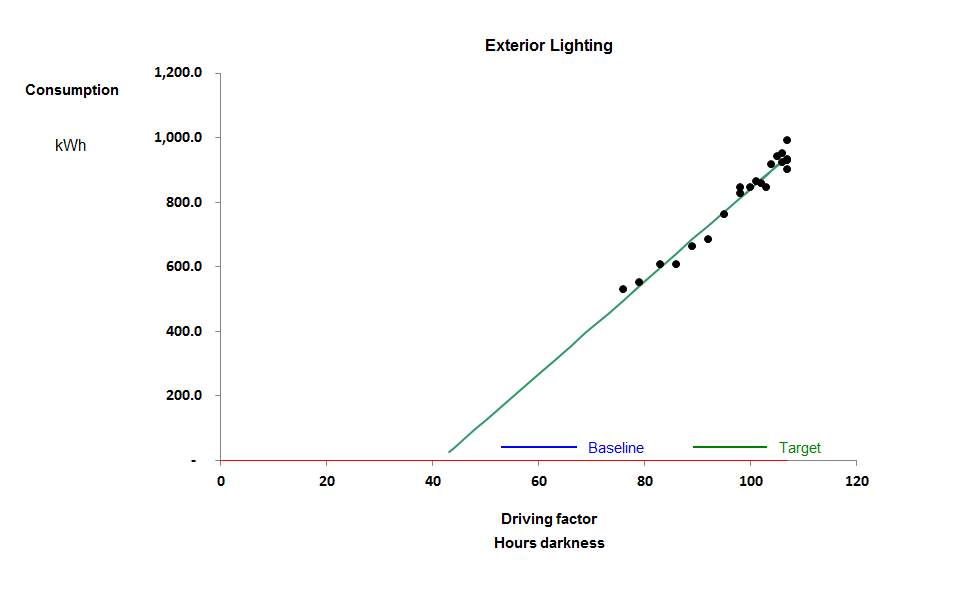The only anomaly is the implied negative intercept, which I will return to later; when you view actual against expected consumption, as below, the relationship seems perfectly rational:

 

Consumption follows the annual sinusoidal profile that you might expect.

But what about that negative intercept? The model appears to predict close to zero consumption in the summer weeks, when there would still be roughly six hours a night of darkness. One explanation could be that the lights are actually habitually turned off in the middle of the night for six hours when there is no activity. That is entirely plausible, and it is a regime that does apply in some places, but not here. For evidence see the ‘heatmap’ view of half-hourly consumption from September to mid November:

 

As you can see, lighting is only off during hours of daylight; note by the way how the duration of daylight gradually diminishes as winter draws on. But the other very clear feature is the difference before and after 26 October when the overnight power level abruptly increased. When I questioned that change, the explanation was rather simple: they had turned on the Christmas lights (you can even see they tested them mid-morning as well on the day of the turn-on).

So that means we must disregard that week and subsequent ones when setting our target for basic external lighting consumption. This puts a different complexion on our regression analysis. If we use only the first four weeks’ data we get the relationship shown with a red line:

In this modified version, the negative intercept is much less marked and the data-points at the top right-hand end of the scatter are anomalous because they include Christmas lighting. There are, in effect, two behaviours here.

The critical lesson we must draw is that regression analysis is just a statistical guess at what is happening: you must moderate the analysis by taking into account any engineering insights that you may have about the case you are analysing