Category Archives: Energy analysis and reporting

Energy analysis and reporting

Energy targeting for humidity-control systems

The amount of moisture in the atmosphere varies through the year because the amount of water vapour that the air can hold is temperature-dependent. We human beings are sensitive to the relative humidity (RH), which is the ratio between the actual moisture content and the maximum that the air could hold at its prevailing temperature: generally, we don’t feel uncomfortable if the RH is between 30% and 70%. Problems will obviously occur in very hot, humid weather (when the RH will be high) but they can also occur in the depths of winter. This is because, if you take some cold outside air and heat it up for use in your building, its relative humidity falls as the temperature increases without the addition of any moisture. In an air-conditioned building, hot outside air is chilled to the comfort temperature, and the RH rises. Suppose that you want to maintain 20°C inside, with RH in the range 40% and 60%. If the ambient air contains less than 0.006 kg of water vapour per kg of dry air (regardless of its temperature), it will need humidifying; but should it exceed 0.009, moisture will need to be removed. The demand for moisture addition or removal will be proportional to the deficit or surplus in the mixing ratio. For example, ambient air at 0.013 kg/kg needs twice as much dehumdification as air at 0.011 kg/kg (0.013-0.009 is double 0.011-0.009).

Figures 1 and 2 show typical weekly histories of moisture deficit and excess for a site in Ireland. Notice how the demand is seasonal, with warmer summer air able to hold more moisture.

Figure 1
Figure 2

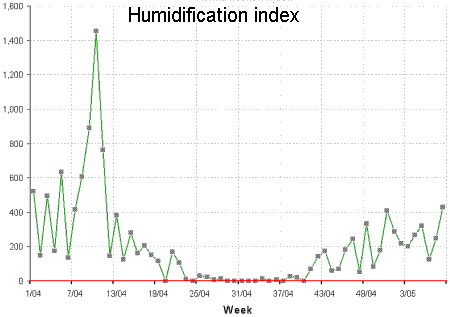
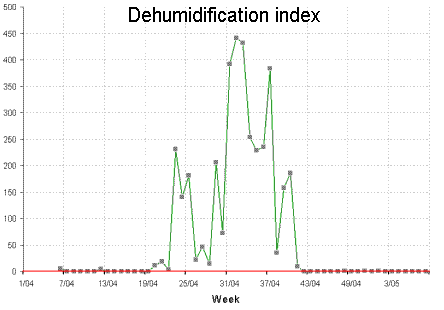
How does this affect energy demand? Well, to dehumidify air you need to chill it to its saturation temperature at the required moisture content. Excess moisture condenses out, and the partially dried air is then reheated to take it back to the required target temperature. This where the extra energy demand comes from.

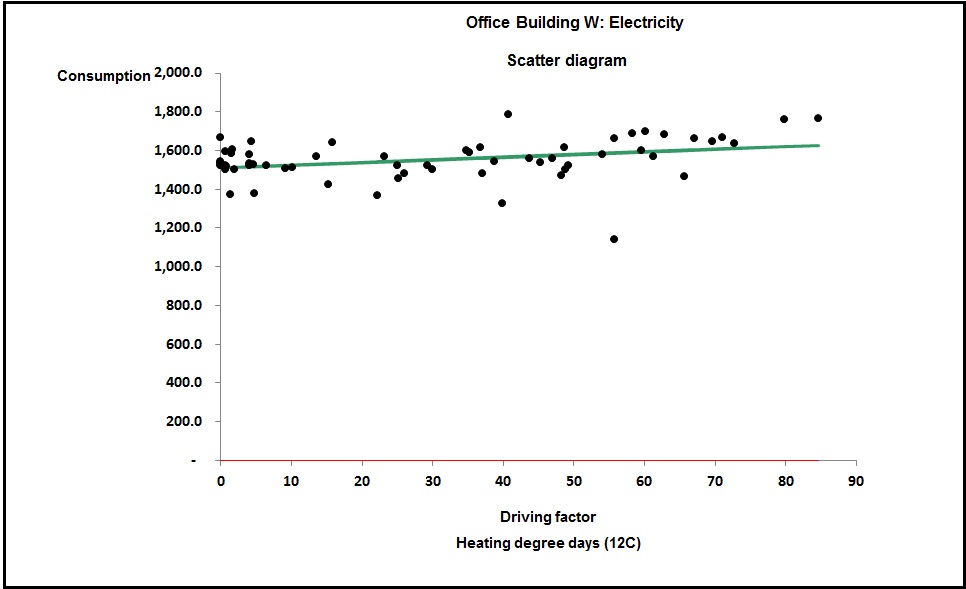
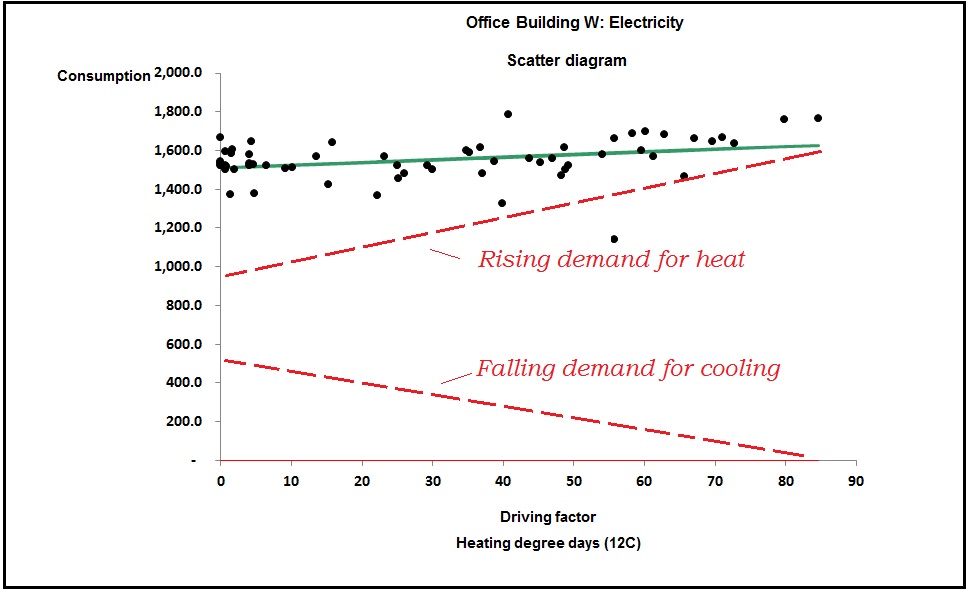
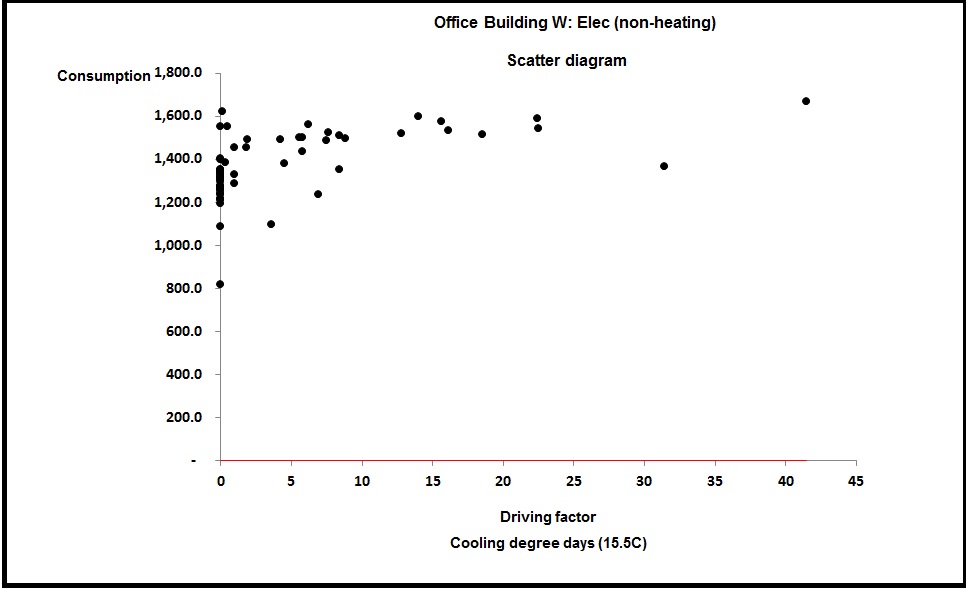
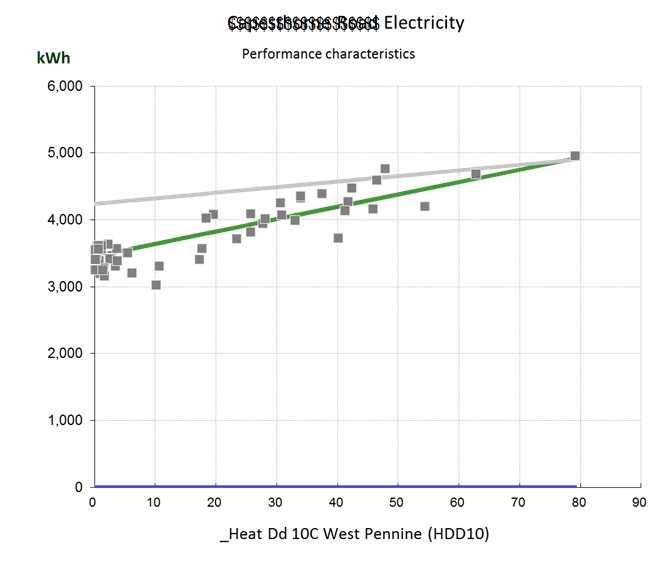
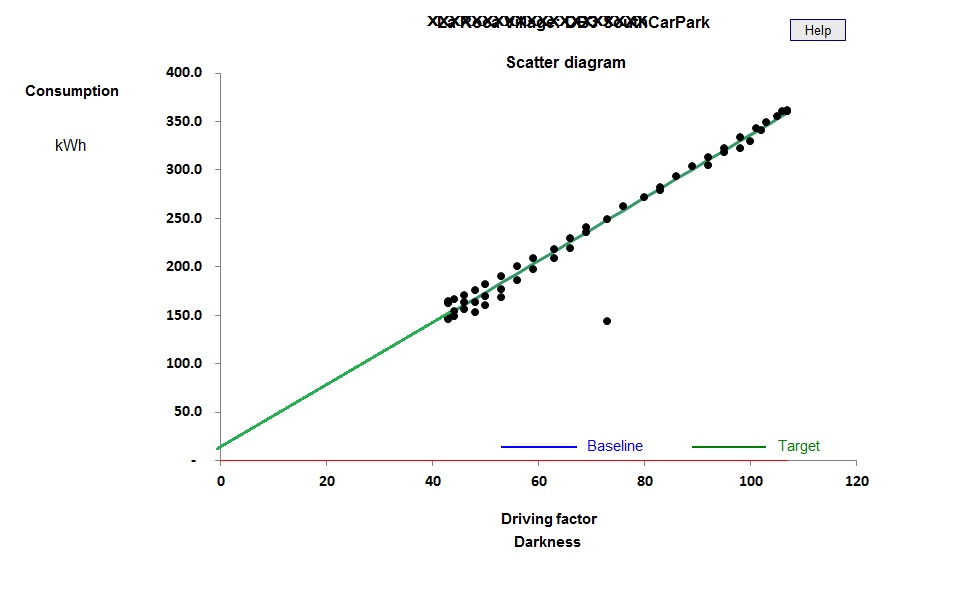
You can see the difference between cooling-only and full air conditioning in figures 3 and 4. Figure 3 shows a case where the relationship between chiller electricity and cooling degree days is evidently a straight line: this building has no humidity control and chiller demand is effectively driven only by the outside dry-bulb temperature.

Figure 3

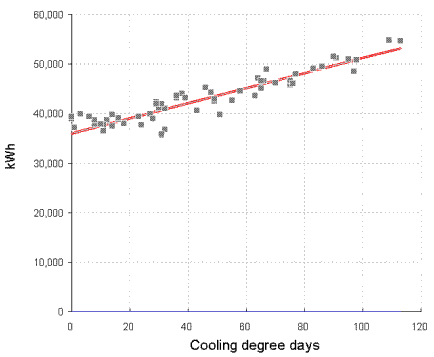
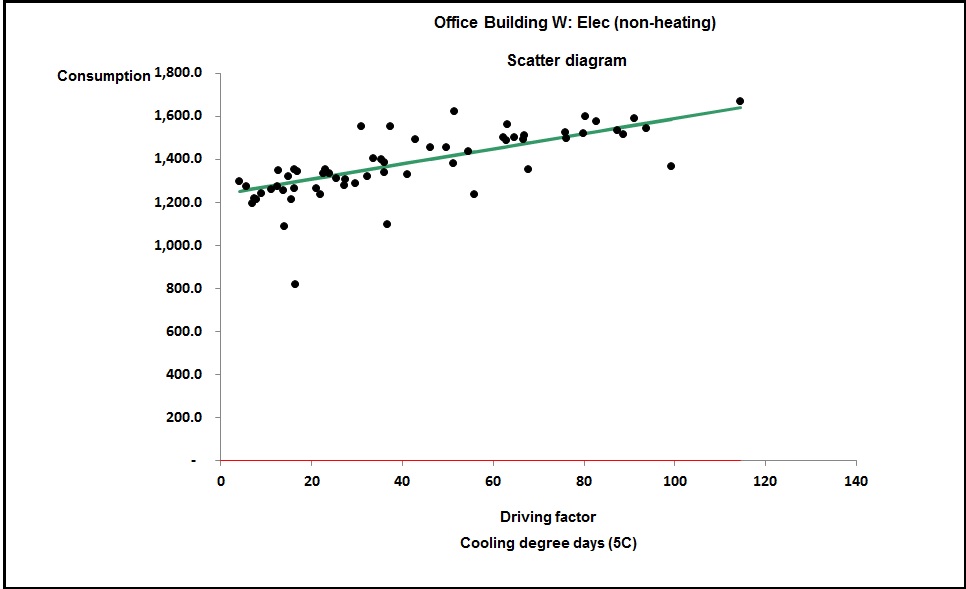
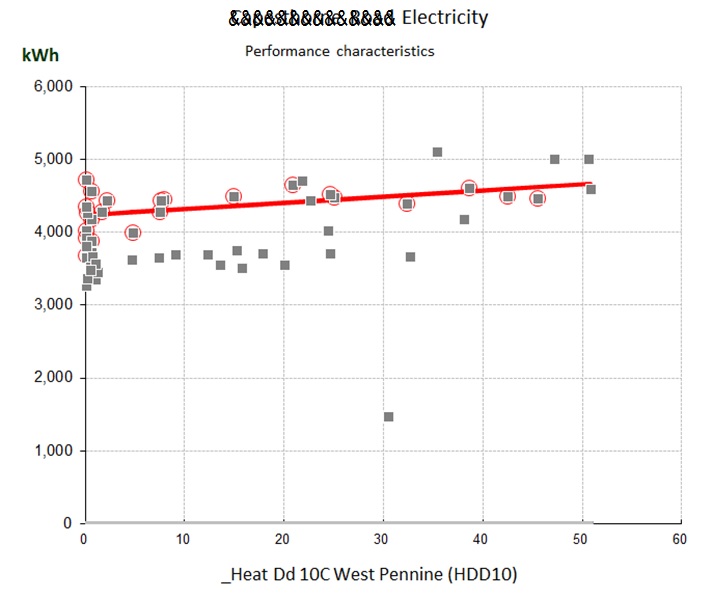
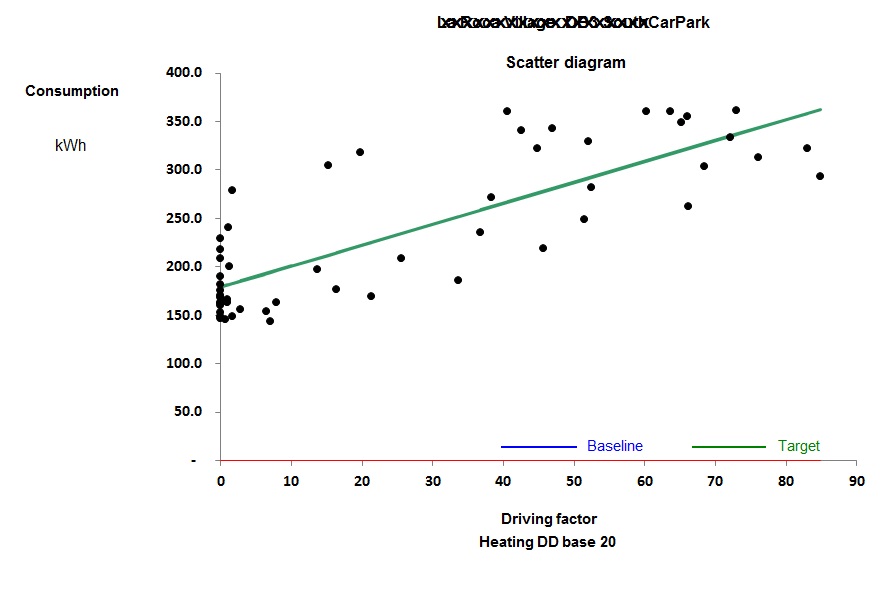
Figure 4, by contrast, is curved; this building has humidity control. The curve occurs because as the weather gets hotter, the amount of moisture in the air increases, and with it the demand for dehumidification.

Figure 4

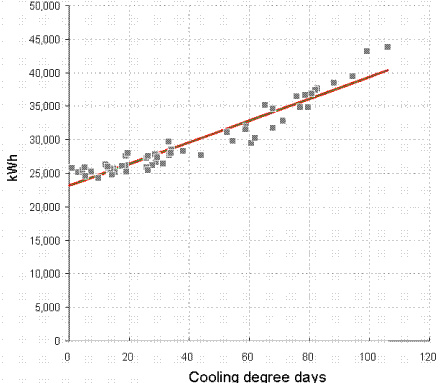
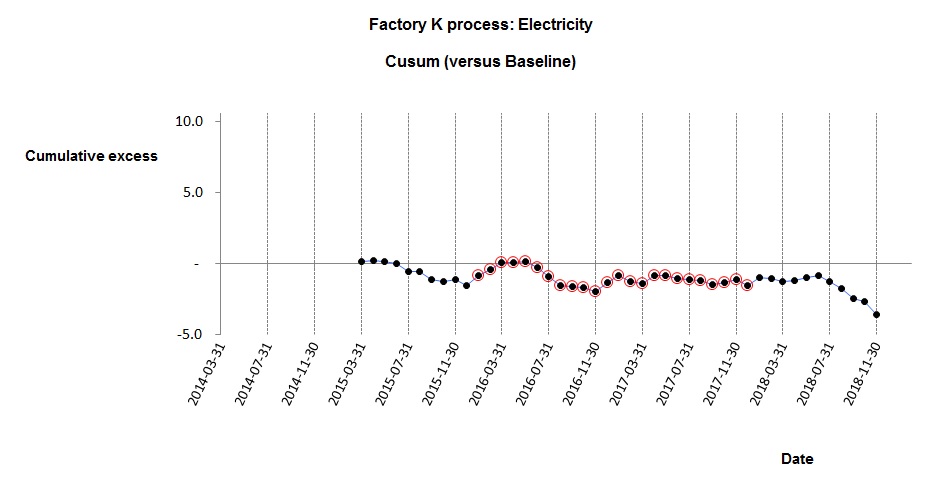
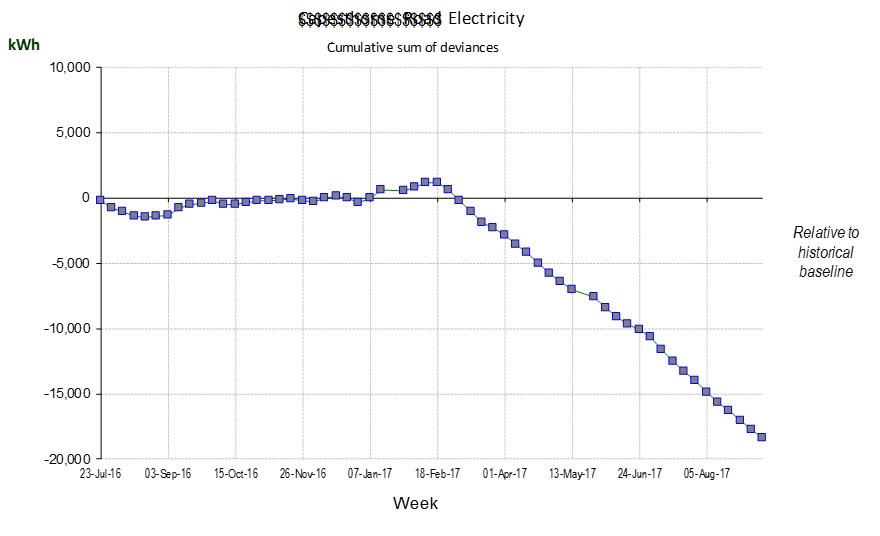
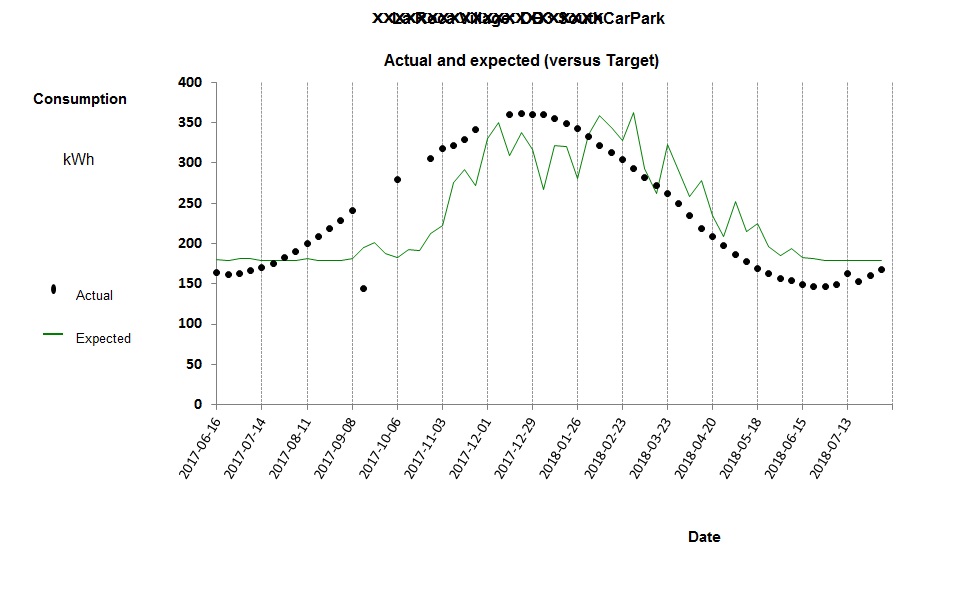
Figure 5 shows the deviation from expected consumption that results when one tries to model electricity demand with the single straight-line relationship of figure 4 in which predicted consumption is

23,151 kWh per week, plus
162 kWh per cooling degree day
Figure 5

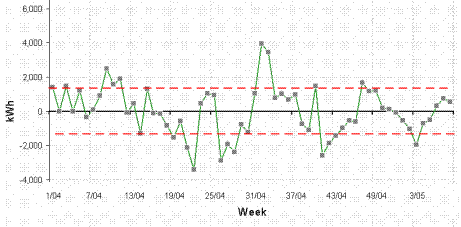
The model can be improved by accounting for the dehumidification demand: Figure 6 shows the history of deviations when a two-factor model is used, in which predicted consumption is

24,259 kWh per week, plus
107 kWh per cooling degree day, plus
16.4 kWh per unit of dehumidification demand
Figure 6

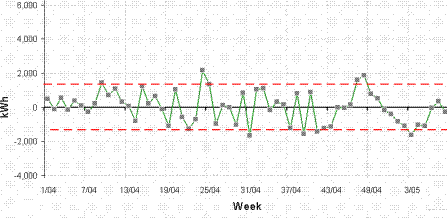
The reduced error in the calculation of expected electricity consumption makes overspend alerts more reliable and the monitoring and targeting scheme more effective.

To implement this scheme one needs local dry-bulb and relative humidity readings at frequent intervals, which are used to calculate the ambient mixing ratio. Two running totals are then kept: one of the accumulated atmospheric moisture deficit, and one of the accumulated excess. The procedure is not unlike the “accumulated temperature deficit” which is used in the calculation of heating degree days.

For details of training courses in energy management visit vesma.com/training

Audits and surveys, Data collection, Energy analysis and reporting, Transport

Tracking performance of light vehicles

Here is a monitoring challenge: suppose you want to do a weekly check on the performance of a small fleet of hotel minibuses. Although you can record the mileage at the end of each week, you will have a lot of error in your fuel measurement because you’ll only know how much fuel was purchased but not when. How can you adjust for the inconsistent fuel tank level at the end of the week?

One method would be to use the trip computer display which will show the estimated remaining miles (see picture). The vehicle in question has a 45-litre tank: at its typical achieved average mpg, it has a range of 613 miles of which it has used 39%, so we can add 45 x 0.39 = 18 litres to our calculated fuel consumption. Note that we will need to deduct an equal amount from next week’s consumption, and this “carry forward” is likely to reduce the error in the adjustment.

This procedure also helps if drivers do not consistently fill to the top. To the extent that they underfill on the last occasion in the week, the shortfall will increase the adjustment volume to compensate. The adjustment can only ever be approximate, however, so it’s better if they consistently brim the tank.

The other advice I would give is to track not miles per gallon (or any similar performance ratio) but to plot a regression line of fuel versus distance. This will pick up, and detect changes in, idling behaviour.

Audits and surveys, Energy analysis and reporting

Monitoring electrically heated and cooled buildings

WHEN you use metered fuel  to heat a building (or indeed if you use the building’s electricity supply, but have no air-conditioning) it is straightforward to monitor heating performance critically because you can relate energy consumption to the weather expressed as degree days.

Things get difficult if you use electricity for both heating and cooling and everything shares a meter, as would be the case if you use reversible heat pumps (air-source or otherwise). Because the seasonal variations in demand for heating and cooling complement each other (one being high when the other is low), you may encounter cases where the sum of the two appears almost constant every week. Such was the case on this 800-m2 office building:

Figure 1: apparent low sensitivity to weather

 

Without going into detail, this relationship implied a heating capacity of little over 1 kW, which is obvious nonsense as there was no other source of heat. The picture had to be caused by overlapping and complementary seasonal demands for heating and cooling, which is illustrated conceptually in Figure 2:

Figure 2: total consumption is the sum of heating and cooling demands

 

The challenge was how to discover the gradients of the hidden heating and cooling lines. The answer in this case lay in the fact that we had sufficient information to estimate the building’s heat rate, which is the net heat flow from the building in watts per unit inside-outside temperature difference (W/K). The heat rate depends on the thermal conductivity of the building envelope and the rate at which outside air enters. There is a formula for the heat rate Q:

Q = Σ(UA) + NV/3

Where U and A are the U-values and superficial areas of each building element (roof, wall, window, etc), V is the volume of the building and N is the number of air changes per hour. Figure 3 shows the spreadsheet in which Q was calculated for the building in question (an on-line tool to do this job is available at vesma.com):

Figure 3: calculation of heat rate

In this case the building measurements were taken from drawings, the U-values were found on the building’s Energy Performance Certificate (EPC), and the figure of 0.5 air changes per hour is just a guess.

The resulting heat rate of 955.5 W/K equates to 955.5 x 24 / 1000  = 22.9 kWh per degree day. This is heat loss from the building but it uses a heat pump and will therefore require less input electricity by a factor of, in this case, 3.77 (that being the coefficient of performance cited on its EPC).  So the input energy required for heating this building is 22.9 / 3.77 = 6.1 kWh per degree day. This is the gradient of the unknown heating characteristic, the upper dotted line in Figure 2.

Need training in energy management? Have a look at vesma.com

To work out the sensitivity to cooling demand we use a little trick. We take the actual consumption history and deduct an allowance for heating load which, in each week, will be 6.1 times the number of heating degree days (remember we just worked out the building needed 6.1 kWh per degree day for heating). This non-heating electricity demand can now be analysed against cooling degree days and this was the result in this case:

Figure 4: variation of non-heating electricity with cooling degree days

 

The gradient of this line is 3.5 kWh per (cooling) degree day. It is of similar order to the 6.1 kWh per degree day for heating, which is to be expected; the building’s heat loss and gain rates per degree difference are likely to be similar. As importantly, we now have an intercept on the vertical axis (a shade over 1,200 kWh per week) which represents the non-weather-related demand. Taking Figure 1 at face value we would have erroneously put the fixed consumption at around 1,500 kWh per week.

Also significant is the fact that Figure 4 was plotted against cooling degree days to a base of only 5°C. That was the only way to get a rational straight line and it means there is a finite amount of cooling going on at outside temperatures down to that value. I had been assured that cooling was only enabled “when the weather got hot”. But plotting demand against cooling degree days to, say, 15.5°C (a common default for summer-only use) gave the result shown in Figure 5:

Figure 5: non-heating electricity demand against cooling degree days to a base of 15.5C

 

This is not as good a correlation as Figure 4 and my conclusion in this case was that when the outside temperature is between 5 and 12°C, this building is likely to have some rooms heating and some cooling.

Energy analysis and reporting, Transport

Carbon emissions – a case of rubbish data and wrong assumptions

The UK Government provides tables for greenhouse gas emissions including generic figures for road vehicles. For example a rigid diesel goods vehicle of 7.5 to 17 tonnes has an indicative figure of 0.601 kg CO2e per km. You need to apply such generic figures with caution, though. I saw a report from a local council that used that particular number to back-calculate emissions from its refuse collection trucks. Leaving aside the fact that many of their vehicles are 26 tonners, they spend much of their time accelerating, braking to a halt, idling and running hydraulic accessories, with the result that one would expect them to do no better than about 4 mpg with emissions more like 1.8 kg CO2e per km, three times the council’s assumed value.

For the council in question that is not a trivial error. Even on their optimistic analysis domestic waste collection represents 33% of their total emissions. Properly calculated (ideally from actual fuel purchases) they will turn out to be more than all their other emissions taken together.

Further reading

Training

For sustainability professionals to make a real practical difference to carbon emissions they need a broad appreciation of technical energy-saving opportunities. To help them understand the potential more clearly I run a one-day course called ‘Energy Efficiency A to Z‘. Details of this can be found at http://vesma.com/training

 

Data collection, Energy analysis and reporting

Justifying additional meters

Additional metering may be required for all sorts of reasons. There are three relatively clear-cut cases where the decision will be dictated by policy:

  • Departmental accountability or tenant billing: it is often held that making managers accountable for the energy consumed in their departments encourages economy. Where this philosophy prevails, departmental sub-metering must be provided unless estimates (which somewhat defeat the purpose) are acceptable. Similar considerations would apply to tenant billing (I am talking about commercial rather than domestic tenants here).
  • Environmental reporting: accurate metering is essential if, for example, consumption data is used in an emissions trading scheme: an assessor could refuse certification if measurements are held to be insufficiently accurate.
  • Budgeting and product costing: this use of meter data is important in industries where energy is a significant component of product manufacturing cost, and where different products (or different grades of the same product) are believed to have different energy intensities.

The fourth case is where metering is contemplated purely for detecting and diagnosing excessive consumption in the context of a targeting and monitoring scheme. This may well be classified as discretionary investment and will require justification. This could be based on a rule of thumb, or on the advice in the Building Regulations (for example). A more objective method is to identify candidates for submetering on the basis of the risk of undetected loss (RoUL). The RoUL method attempts to quantify the absolute amount of energy that is likely to be lost through inability to detect adverse changes in consumption characteristics. It comprises four steps for each candidate branch:

  1. Estimate the annual cost of the supply to the branch in question (see below).
  2. Decide on the level of risk (see table below) and pick the corresponding factor.
  3. Multiply the cost in step 1 by the factor in step 2, to get an estimate of the annual average loss.
  4. Use the result from step 3 to set a budget limit for installing, reading and maintaining the proposed meter.
Risk Typical characteristics Suggested
factor*
High Usually associated with highly-intermittent or very variable loads under manual control, or under automatic control at unattended installations (the risk is that equipment is left to run continually when it should only run occasionally, or is allowed to operate ‘flat out’ when its output ought to modulate in response to changes in demand). Examples of highly-intermittent loads include wash-down systems, transfer pumps, frost protection schemes, and in general any equipment which spends significant time on standby. Typical continuous but highly-variable loads would include space heating and cooling systems. It should be borne in mind that oversized plant, or any equipment which necessarily runs at low load factor, is at increased risk. 20%
Medium Typified by variable loads and intermittently-used equipment operating at high load factor under automatic control, in manned situations where failure of the automatic controls would probably become apparent quickly. 5%
Low Anything which necessarily runs at high load factor (and therefore has little capacity for excessive operation) or where loss or leakage, if able to occur at all, would be immediately detected and rectified. 1%

*Note: the risk percentages are suggested only; the reader should use his or her judgment in setting percentages appropriate to individual circumstances

The RoUL method tries to quantify the cost of not having a meter, but this relies on knowing the consumption in the as-yet-unmetered circuit. The circular argument has to be broken by estimating consumption:

  • by step testing
  • using regression analysis to determine sensitivity to driving factors such as product throughput and prevailing weather
  • using ammeter readings for electricity, condensate flow for steam, etc.
  • multiplying installed capacity by assumed (or measured) load factors
  • from temporary metering
Energy analysis and reporting

Uncertainty in savings estimates: a worked example

To prove that energy performance has improved, we calculate the energy performance indicator (EnPI) first for a baseline period and again during the subsequent period which we wish to evaluate. Let us represent the baseline EnPI value as P1 and the subsequent period’s value as P2

Most people would then say that as long as P2 is less than P1 we have proved the case. But there is uncertainty in both P1 and P2 and this will be translated into uncertainty in the estimate of their difference. We strictly need to show not only that the difference (P1 – P2) is positive, but that the difference exceeds the uncertainty in its calculation. Here’s how we can do that.

In the example which follows I will use a particular form of EnPI called the ‘Energy Performance Coefficient’ (EnPC), although any numerical indicator could be used. The EnPC is the ratio of actual to expected consumption. By definition this has a value of 1.00 over your baseline period, falling to lower values if energy-saving measures result in consumption less than otherwise expected. To avoid a long explanation of the statistics I’ll also draw on Appendix B of the International Performance Measurement and Verification Protocol (IPMVP, 2012 edition) which can be consulted for deeper explanations.

IPMVP recommends evaluation based on the Standard Error, SE, of (in this case) the EnPC. To calculate SE you first calculate the EnPC at regular intervals and measure the Standard Deviation (SD) of the results; then divide SD by the square root of the number of EnPI observations. In my sample data I use 2016 and 2017 as the baseline period, and calculate the EnPC month by month.

In my sample data the standard deviation of the EnPC during the baseline period was 0.04423 and there being 24 observations the baseline Standard Error was thus

SE1 = 0.04423 / √24 = 0.00903

Here is the cusum analysis with the baseline observations highlighted:

The cusum analysis shows that performance continued unchanged after the baseline period but then in July 2018 it improved. We see that the final five months show apparent improvement; the mean EnPC after the change was 0.94, and these five observations had a Standard Deviation of 0.02402. Their Standard Error was therefore

SE2 = 0.02402 / √5 = 0.01074

SEdiff , the Standard Error of the difference (P1 – P2) is given by

SEdiff = √( SE12 + SE22 )

= √( 0.009032 + 0. 010742 )

= 0.01403

SE on its own does not express the true uncertainty. It must be multiplied by a safety factor t which will be smaller if we have more observations (or if we can accept lower confidence) and vice versa. This table is a subset of t values cited by IPMVP:

	     |     Confidence level     |
             |   90%  |   80%  |   50%  |
Observations |        |        |        |
      5      |  2.13  |  1.53  |  0.74  |
     10      |  1.83  |  1.38  |  0.70  |
     12      |  1.80  |  1.36  |  0.70  |
     24      |  1.71  |  1.32  |  0.69  |
     30      |  1.70  |  1.31  |  0.68  |

Let us suppose we want to be 90% confident that the true reduction in the EnPC lies within a certain range. We therefore need to pick a t-value from the “90%” column of the table above. But do we pick the value corresponding to 24 observations (the baseline case) or 5 (the post-improvement period)? To be conservative—as required by IPMVP—we take the lower number, meaning we must in this case use a t value of 2.13.

Now in the general case ∆P, the EnPC reduction, is given by

∆P = (P1 – P2) ± t.SEdiff

Which, substituting the values from our example, would yield

∆P = (1.00 – 0.94) ± (2.13 x 0.01403)

∆P = 0.06 ± 0.03

The lowest probable value of the improvement ∆P is thus (0.06 – 0.03) = 0.03 . It may in reality be less, but the chances of that are only 1 in 20 because we are 90% confident that it falls within the stated range and by implication 5% confident that it is above the upper limit.

Footnote: example data

The analysis is based on real data (preview below). These are from an anonymous source and  multiplied by a secret factor to disguise their true values. Anybody wishing to verify the analysis can download the anonymous data as a spreadsheet here.

Note: to compute the baseline EnPC

  1. do a regression of MWh against tonnes using the months labelled ‘B’
  2. create a column of ‘expected’ consumptions by substituting tonnage values in the regression formula 
  3. divide each actual MWh figure by the corresponding expected value

Energy analysis and reporting, Project profiles

Bulk measurement and verification

Anyone familiar with the principles of monitoring and targeting (M&T) and measurement and verification (M&V) will recognise the overlap between the two. Both involve establishing the mathematical relationship between energy consumption and one or more independently-variable ‘driving factors’, of which one important example would be the weather expressed numerically as heating or cooling degree days.

One of my clients deals with a huge chain of retail stores with all-electric services. They are the subject of a rolling refit programme, during which the opportunity is taken to improve energy performance. Individually the savings, although a substantial percentage, are too small in absolute terms to warrant full-blown M&V. Nevertheless he wanted some kind of process to confirm that savings were being achieved and to estimate their value.

My associate Dan Curtis and I set up a pilot process dealing in the first instance with a sample of a hundred refitted stores. We used a basic M&T analysis toolkit capable of cusum analysis and regression modelling with two driving factors, plus an overspend league table (all in accordance with Carbon Trust Guide CTG008). Although historical half-hourly data are available we based our primary analysis on weekly intervals.

The process

The scheme will work like this. After picking a particular dataset for investigation, the analyst will identify a run of weeks prior to the refit and use their data establish a degree-day-related formula for expected consumption. This becomes the baseline model (note that in line with best M&V practice we talk about a ‘baseline model’ and not a baseline quantity; we are interested in the constant and coefficients of the pre-refit formula). Here is an example of a store whose electricity consumption was weakly related to heating degree days prior to its refit:

Cusum analysis using this baseline model yields a chart which starts horizontal but then turns downwards when the energy performance improves after the refit:

Thanks to the availability of half-hourly data, the M&T software can display a ‘heatmap’ chart showing half-hourly consumption before, during and after the refit. In this example it is interesting to note that savings did not kick in until two weeks after completion of the refit:

Once enough weeks have passed (as in the case under discussion) the analyst can carry out a fresh regression analysis to establish the new performance characteristic, and this becomes the target for every subsequent week. The diagram below shows the target (green) and baseline (grey) characteristics, at a future date when most of the pre-refit data points are no longer plotted:

A CTG008-compliant M&T scheme retains both the baseline and target models. This has several benefits:

  • Annual savings can be projected fairly even if the pre- or post-refit periods are less than a year;
  • The baseline model enables savings to be tracked objectively: each week’s ‘avoided energy consumption’ is the difference between actual consumption and what the baseline model yielded as an estimate (given the prevailing degree-day figures); and
  • The target model provides a dynamic yardstick for ongoing weekly consumptions. If the energy-saving measures cease to work, actual consumption will exceed what the target model predicts (again given the prevailing degree-day figures). See final section below on routine monitoring.

I am covering advanced M&T methods in a workshop on 11 September in Birmingham

A legitimate approach?

Doing measurement and verification this way is a long way off the requirements in IPMVP. In the circumstances we are talking about – a continuous pipeline of refits managed by dozens of project teams – it would never be feasible to have M&V plans for every intervention,. Among the implications of this is that no account is taken (yet) of static factors. However, the deployment of heat-map visualisations means that certain kinds of change (for example altered opening hours) can be spotted easily, and others will be evident. I would expect that with the sheer volume of projects being monitored, my client will gradually build up a repertoire of common static-factor events and their typical impact. This makes the approach essentially a pragmatic one of judging by results after the event; the antithesis of IPMVP, but much better aligned to real-world operations.

Long-term routine monitoring

The planned methodology, particularly when it comes to dealing with erosion of savings performance, relies on being able to prioritise adverse incidents. Analysts should only be investigating in depth cases where something significant has gone wrong. Fortunately the M&T environment is perfect for this,  since ranked exception reporting is one of its key features. Every week, the analyst will run the Overspend League Table report which ranks any discrepancies in descending order of apparent weekly cost:

Any important issues are therefore at the top of page 1, and a significance flag is also provided: a yellow dot indicating variation within normal uncertainty bands, and a red dot indicating unusually high deviation. Remedial effort can then be efficiently targeted, and expected-consumption formulae retuned if necessary.

Energy analysis and reporting

Monitoring external lighting

The diagram below shows the relationship, over the past year, between weekly electricity consumption and the number of hours of darkness per week for a surface car park. It is among the most consistent cases I have ever seen:

Figure 1: relationship between kWh and hours of darkness

 

 

There is a single outlier (caused by meter error).

Although both low daylight availability and cold weather occur in the winter, heating degree days cannot be used as the driving factor for daylight-linked loads.  Plotting the same consumption data against heating degree days gives a very poor correlation:

Figure 2: relationship between kWh and heating degree days

There are two reasons for the poor correlation. One is the erratic nature of the weather (compared with very regular variations in daylight availability) and the other is the phase difference of several weeks between the shortest days and the coldest weather. If we co-plot the data from Figure 2 as a time-series chart we see this illustrated perfectly. In Figure 3 the dots represent actual electricity consumption and the green trace shows what consumption was predicted by the best-fit relationship with heating degree days:

Figure 3: actual kWh compared with a weather-linked model of expected consumption

Compare Figure 3 with the daylight-linked model:

Figure 4: actual and expected kWh co-plotted using daylight-linked model

One significant finding (echoed in numerous other cases) is that it is not necessary to measure actual hours of darkness: standard weekly figures work perfectly well. It is evident that occasional overcast and variable cloud cover do not introduce perceptible levels of error. Moreover, figures for UK appear to work acceptably at other latitudes: the case examined here is in northern Spain (41°N) but used my standard darkness-hour table for 52°N.

You can download my standard weekly and monthly hours-of-darkness tables here.

This article is promoting my advanced energy monitoring and targeting workshop in Birmingham on 11 September

 

 

Energy analysis and reporting

Using M&T techniques on billing patterns

One of my current projects is to help someone with an international estate to forecast their monthly energy consumption and hence develop a monthly budget profile. Their budgetary control will be that much tighter because it has seasonality built in to it in a realistic fashion.

Predicting kWh consumptions at site level is reasonably straightforward because one can use regression analysis against appropriate heating and cooling degree-day values, and then extrapolate using (say) ten-year average figures for each month. The difficulty comes in translating predicted consumptions into costs. To do this rigorously one would mimic the tariff model for each account but apart from being laborious this method needs inputs relating to peak demand and other variables, and it presumes being able to get information from local managers in a timely manner. To get around these practical difficulties I have been trying a different approach. Using monthly book-keeping figures I analysed, in each case, the variation in spend against the variation in consumption. Gratifyingly, nearly all the accounts I looked at displayed a straight-line relationship, i.e., a certain fixed monthly spend plus a flat rate per kWh. Although these were only approximations, many of them were accurate to half a percent or so. Here is an example in which the highlighted points represent the most recent nine months, which are evidently on a different tariff from before:

I am not claiming this approach would work in all circumstances but it looks like a promising shortcut.

Cusum analysis also had a part to play because it showed if there had been tariff changes, allowing me to limit the analysis to current tariffs only.

The methods discussed in this article are taught as part of my energy monitoring and targeting courses: click here for details

Furthermore, in one or two instances there were clear anomalies in the past bills where spends exceeded what would have been expected. This suggests it would be possible to include bill-checking in a routine monitoring and targeting scheme without the need for thorough scrutiny of contract tariffs.

Energy analysis and reporting

Data centres and ISO 50001

Certification to ISO50001 can yield benefits but would be fatally compromised if a misleading energy performance indicator is used to track progress.

Power Utilisation Effectiveness, PUE, is the data-centre industry’s common way of reporting energy performance, but it does not work. It is distorted by weather conditions and (worse still) gives perverse results if users improve the energy efficiency of the IT equipment housed in a centre through (for example) virtualisation.

This presentation given at Data Centres North in May 2018 explains the problem and shows how a corrected PUE should be computed.