In energy-intensive manufacturing processes there is a need to benchmark production units against each other and against yardstick figures. Conventional wisdom has it that you should compare specific energy ratios (SER), of which kWh per gross tonne is one common example. It seems simple and obvious but, as anybody will know who has tried it, it does not really work because a simple SER varies with output, and this clouds the picture.

To illustrate the problem and to suggest a solution, this article picks some of the highlights from a pilot exercise to benchmark air compressors. These are the perfect thing for the purpose not least because they are universally used and obey fairly straightforward physical laws. Furthermore, because they are all making a similar product from the same raw material, they should in principle be highly comparable with each other.

Various conventions are used for expressing compressors’ SERs but I will use kWh per cubic metre of free air. From the literature on the subject you might expect a given compressor’s SER to fall in the range 0.09 to 0.14 kWh/m³ (typically). Lower SER values are taken to represent better performance.

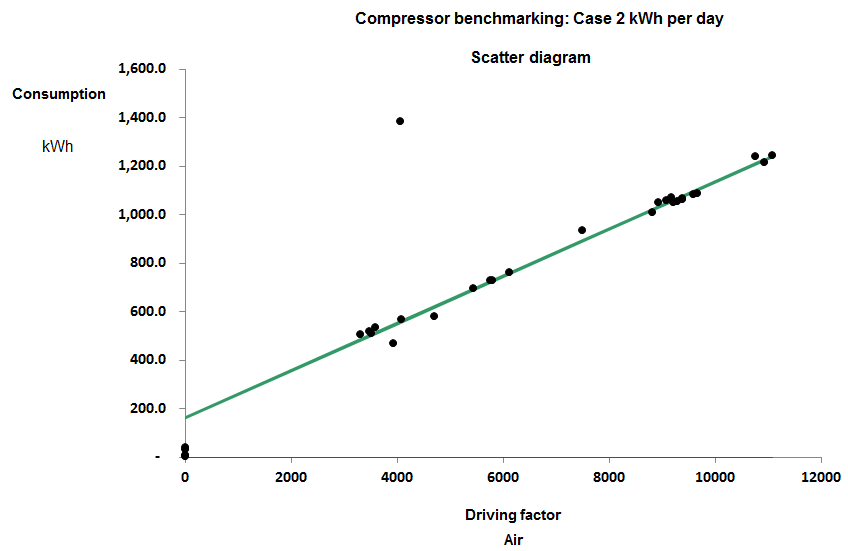
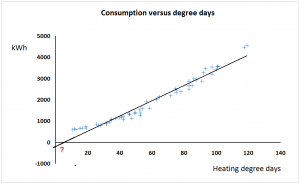
The drawback of the SER approach is that some compressor installations, like any energy-intensive process, have a certain fixed standing load independent of output. The compressor installation in Figure 1 has a standing load of 161 kWh per day for example, and this has a distorting effect: if you divide kWh by output at an output of 9,000 m³ you should find the SER is just under 0.12 kWh/m³ but at a low daily output, say 4,000 m³ , you get 0.14 kWh/m³. The fixed consumption makes performance look more variable than it really is and changes in throughput change the SER whereas in reality, with a small number of obvious exceptions, the performance of this particular compressor looks quite consistent.

Figure 1

When I say it looks consistent I mean that consumption has a consistent straight-line relationship with output. The gradient of the best-fit straight line does not change across the normal operating range: it is said to be a ‘parameter’. In parametric benchmarking we compare compressors’ marginal SERs, that is, the gradients of their energy-versus-output scatter diagrams. The other parameter that we might be interested in is the standing load, i.e., where the diagonal characteristic crosses the vertical (kWh) axis.

The compressor installation in Figure 1 is one of eight that I compared in a pilot study whose results were as follows:

============================
Case   Marginal  Standing 
No     SER       kWh per day
----------------------------
 8      0.085       115 
 5      0.090        62 
 1      0.092     3,062 
 2      0.097       161 
 7      0.105        58 
 6      0.124        79 
 3      0.161       698 
============================

As you can see, the marginal SERs are mainly fairly comparable and may prove to be more so once we have taken proper account of inlet temperatures and delivery pressures. But their standing kWh per day are wildly different. It makes little sense to try comparing the standing loads. In part they are a function of the scale of the installation (Case 1 is huge) but also the metering may be such that unrelated constant-ish loads are contributing to the total. The variation in energy with variation in output is the key comparator.

In order to conduct this kind of analysis, one needs frequent meter readings, and the installations in the pilot study were analysed using either daily or weekly figures (although some participants provided minute-by-minute records). Rich data like this can be filtered using cusum analysis to identify inconsistencies, so for example in Case 3, although there is no space to go into the specific here, we found that performance tended to change dramatically from time to time and the marginal SER quoted in the table is the best that was consistently achieved.

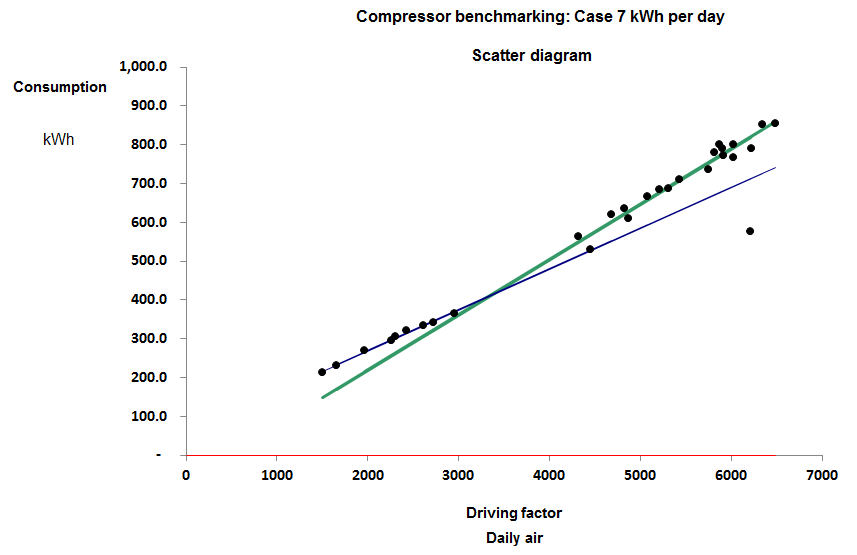
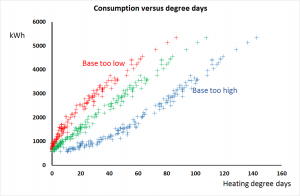
Case 7 was found to toggle between two different characteristics depending on its loading: see Figure 2. At higher outputs its marginal SER rose to 0.134 kWh/m³, reflecting the relatively worse performance of the compressors brought into service to match higher loads.

Figure 2

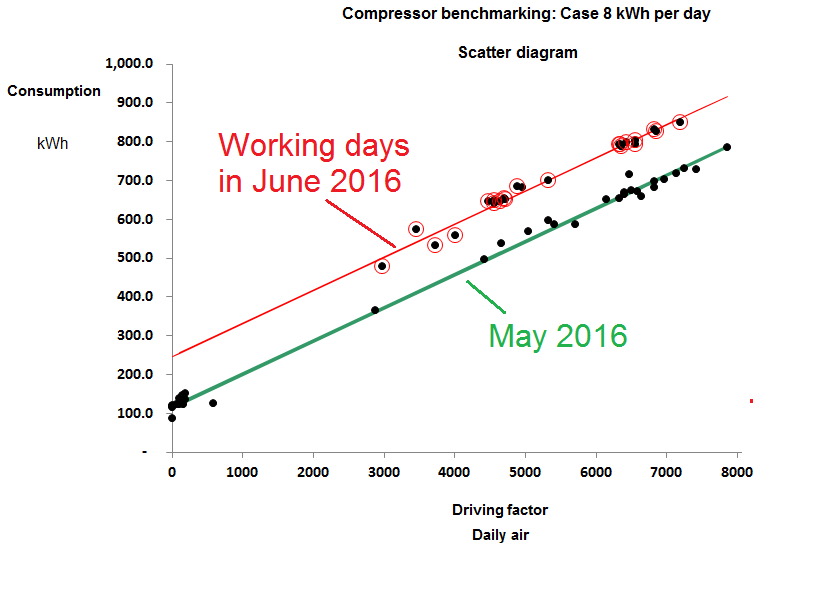
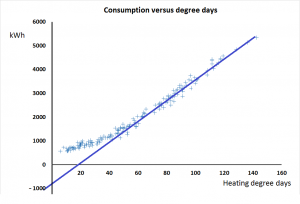
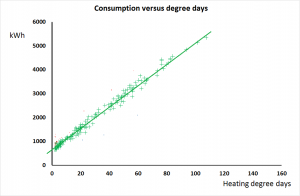
In Case 8, meanwhile, the compressor plant changed performance abruptly at the start of June, 2016. Figure 3 compares performance in May with that on working days in June and we obtained the following explanation. The plant consists of three compressors. No.1 is a 37 kW variable-speed machine which takes the lead while Nos 2 and 3 are identical fixed-speed machines also of 37 kW rating. Normally, No.2 takes the load when demand is high but during June they had to use No.3 instead and the result was a fixed additional consumption of 130 kWh per day. The only plausible explanation is that No. 3 leaks 63 m³ per day before the meter, quite possibly internally because of defective seals or non-return vales. Enquiries with the owner revealed that they had indeed been skimping on maintenance and they have now had a quote to have the machines overhauled with an efficiency guarantee.

Figure 3

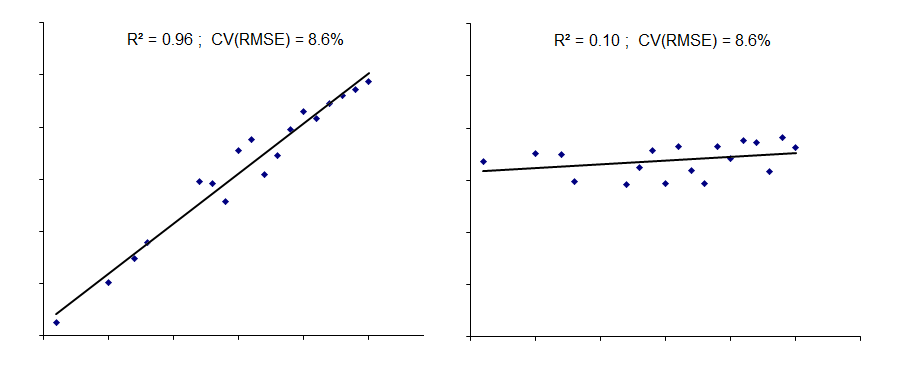
This last case is one of three where we found variations in performance through time on a given installation and were able to isolate the period of best performance. It improves a benchmarking exercise if one can focus on best achievable, rather than average, performance; this is impossible with the traditional SER approach, as is the elimination of rogue data. Nearly all the pilot cases were found to include clear outliers which would have contaminated a simple SER.

Deliberately excluding fixed overhead consumption from the analysis has two significant benefits:

• It enables us to compare installations of vastly differing sizes, and
• it means we can tolerate unrelated equipment sharing the meter as long as its contribution to demand is reasonably constant.

In statistical analysis the coefficient of determination (more commonly known as R²) is a measure of how well variation in one variable explains the variation in something else, for instance how well the variation in hours of darkness explains variation in electricity consumption of yard lighting.

R² varies between zero, meaning there is no effect, and 1.0 which would signify total correlation between the two with no error. It is commonly held that higher R² is better, and you will often see a value of (say) 0.9 stated as the threshold below which you cannot trust the relationship. But that is nonsense and one reason can be seen from the diagrams below which show how, for two different objects,  energy consumption on the vertical or y axis might relate to a particular driving factor or independent variable on the horizontal or x axis.

In both cases, the relationship between consumption and its driving factor is imperfect. But the data were arranged to have exactly the same degree of dispersion. This is shown by the CV(RMSE) value which is the root mean square deviation expressed as a percentage of the average consumption.  R² is 0.96  (so-called “good”) in one case but only 0.10 (“bad”) in the other. But why would we regard the right-hand model as worse than the left? If we were to use either model to predict expected consumption, the absolute error in the estimates would be the same.

By the way, if anyone ever asks how to get R² = 1.0 the answer is simple: use only two data points. By definition, the two points will lie exactly on the best-fit line through them!

Another common misconception is that a low value of R² in the case of heating fuel signifies poor control of the building. This is not a safe assumption. Try this thought experiment. Suppose that a building’s fuel consumption is being monitored against locally-measured degree days. You can expect a linear relationship with a certain R² value. Now suppose that the local weather monitoring fails and you switch to using published degree-day figures from a meteorological station 35km away. The error in the driving factor data caused by using remote weather observations will reduce R² because the estimates of expected consumption are less accurate; more of the apparent variation in consumption will be attributable to error and less to the measured degree days. Does the reduced R²  signify worse control? No; the building’s performance hasn’t changed.

Footnote: for a deeper, informative and highly readable treatment of this subject see this excellent paper by Mark Stetz. 

When considering the consumption of fuel for space heating, the degree-day base temperature is the outside air temperature above which heating is not required, and the presumption is that when the outside air is below the base temperature, heat flow from the building will be proportional to the deficit in degrees. Similar considerations apply to cooling load, but for simplicity this article deals only with heating.

In UK practice, free published degree-day data have traditionally been calculated against a default base temperature of 15.5°C (60°F). However, this is unlikely to be truly reflective of modern buildings and the ready availability of degree-day data to alternative base temperatures makes it possible to be more accurate. But how does one identify the correct base temperature?

The first step is to understand the effect of getting the base temperature wrong. Perhaps the most common symptom is the negative intercept that can be seen in Figure 1 which compares the relationships between consumption and degree days. This is what most often alerts you to a problem:

It should be evident that in Figure 1 we are trying to fit a straight line to what is actually a curved characteristic. The shape of the curve depends on whether the base temperature was too low or too high, and Figure 2 shows the same consumptions plotted against degree days computed to three different base temperatures: one too high (as Figure 1), one too low, and one just right.

Notice in Figure 2 that the characterists are only curved near the origin. They are parallel at their right-hand ends, that is to say, in weeks when the outside air temperature never went above the base temperature. The gradients of the straight sections are all the same, including of course the case where the base temperature was appropriate. This is significant because although in real life we only have the distorted view represented by Figure 1, we now know that the gradient of its straight section is equal to the true gradient of the correct line.

So let’s revert to our original scenario: the case where we had a single line where the base temperature was too high. Figure 3 shows that a projection of the straight segment of the line intersects the vertical axis at -1000 kWh per week, well below the true position, which from Figure 1 we can judge to be around 500 kWh per week. The gradient of the straight section, incidentally, is 45 kWh per degree day.

To correct the distortion we need to shift the line in Figure 3 to the left by a certain number of degree days so that it ends up looking like Figure 4 below. The change in intercept we are aiming for is 1,500 kWh (the difference between the apparent intercept of -1000, and the true intercept, 500*). We can work out how far left to move the line by dividing the required change in the intercept by the gradient: 1500/45 = 33.3 degree days. Given that the degree-day figures are calculated over a 7-day interval, the required change in base temperature is 33.3/7 = 4.8 degrees

Note that only the points in the straight section moved the whole distance to the left: in the curved sections, the further left the point originally sits, the less it moves. This can best be visualised by looking again at Figure 2.

In more general terms the base-temperature adjustment is given by (Ct-Ca)/m.t where:

Ct is the true intercept;
Ca is the apparent intercept when projecting the straight portion of the distorted characteristic;
m is the gradient of that straight portion; and
t is the observing-interval length in days

* The intercept could be judged or estimated by a variety of methods including: empirical observations like averaging the consumption in non-heating weeks; by ‘eyeball’; or by fitting a curved regression line, etc..

The FlexDD service from Degree Days Direct is a framework for delivering degree-day data. It allows you to create Excel energy workbooks with degree-day tables in them which update themselves automatically from the cloud.

Having subscribed to the observing stations you require, you’ll receive an Excel workbook linked to your account with some initial tables built in which you can customise as required.

This is a typical Excel table. In each column you specify the observing station (a), heating or cooling mode (b), and base temperature (c). Put datestamps at (d) and copy the output formulae into the table (e).

Available base temperatures for heating are at whole-number increments from 10°C to 25°C For cooling the range is 5°C to 30°C. For compatibility with legacy reports, additional base temperatures of 15.5°C and 18.5°C heating and 15.5°C cooling are also provided.

You can clone the worksheet to have both monthly and weekly reports if you wish, and your weekly reports can end on any day of the week.

Pricing

There is an initial setup charge of £50, with per-station subscription charges of £12 per annum. Prices exclude VAT. Orders can be placed by emailing .

A reader contacted me to say that he had a gas meter on his site that runs backwards when there is no demand. It is a rotary positive-displacement type (see picture) and I believe it is one of a number of sub-meters on what I know to be a sprawling industrial complex. His first thought had been that the gas in the downstream pipework might be warming up and expanding, pushing back through the meter, but a quick calculation showed that this would only account for about 10% of the observed volume. We established that the meter was in the right way around, and had mechanical as well as digital readouts, which tallied with each other. I put the puzzle to the readers of the Energy Management Register to see what they thought. I got about twenty responses and here is an edited summary of what came back.

A few people asked questions and suggested some measurements that might be useful: for example wanting to know what sizes and types of equipment were on the network, and what the standing pressures were upstream and downstream of the meter (it can only run backwards if the downstream pressure is higher than upstream). One theory was that there is something pressurising the downstream side. This is not completely fanciful and one reader on a similar site mentioned that he had gas supplies at both ends, one of which had been capped off. A long-forgotten redundant but imperfectly-isolated second mains supply could easily be the culprit. On a big network it would feed back through the meter and into other branches if there is even the slightest pressure differential.

Another reader asked if there were any gas booster sets downstream of the meter, fitted to increase gas pressure above that of the supply main on high-output burners. When the burners shut off, any residual pressure could dissipate via a defective non-return valve back through the meter.

A lot of respondents asked no questions but fired off some inspired suggestions. One raised the possibility that groundwater was leaking into buried pipework and displacing gas. It would not need to be very deep for this to happen but presumably there would be obvious and dramatic consequences whenever the burners fired up after a prolonged idle spell. Several raised the possibility that air was being pumped in somehow — which could create a gas mixture that could detonate rather than ignite when next called on.

Other readers focussed on the upstream gas pressure and the possibility that something might be causing it to drop. For example, it  might be cooling down during periods of no demand. If the upstream pipework is extensive this could draw back a larger volume via the meter than expansion downstream but this would have only a temporary effect, and only when other branches were not drawing gas. Two or three people raised the possibility that there were gas booster sets in the other upstream branches and that the suction from those would depress the upstream pressure. Indeed one reader had seen exactly this effect trip out a CHP plant on low pressure. Two ingenious folk suggested a Bernoulli effect, in which the problematic supply is teed off from a main and high-velocity gas passing the junction sucks gas from the branch.

One reader thought that the meter ought to be fitted with a ratchet to stop it turning backwards; I think this is normal with fiscal meters for obvious reasons, and it is not a bad point. If you stall a gear meter like the one in question, it stops the flow, and as there are safety implications in many of the ideas put forward, that seems like a good idea.

At the time of writing we are waiting to find out what was discovered. Meanwhile thanks to Bill Gysin, Mike Mann, Mike Muscott, Andrew Cowan, Vic Tuffen, Ben Davies-Nash, Jeremy Draper, James Pollington, John Perkin, Alan Turner, Bill Spragg, Mike Bond, Jonathan Morgan, James Ferguson, Neil Howison, Ian Hill, Tony Duffin, Neil Alcock, Peter Thompson  and others for your insights.

League tables are highly unsuitable for reporting energy performance, because small measurement errors can propel participants up and down the table. As a result, the wrong people get praised or blamed, and real opportunities go missing while resources are wasted pursuing phantom problems.

To illustrate this, let’s look at a fashionable application for league tables: driver behaviour. The table on the right (Figure 1) shows 26 drivers, each of whom is actually achieving true fuel economy between 45 and 50 mpg in identical vehicles doing the same duties. This is a very artificial scenario but to make it a bit more realistic let us accept that there will be some error in measurement: alongside their ‘true’ mpg I have put the ‘measured’ values. These differ by a random amount from the true value, on a normal distribution with a standard deviation of 1 mpg — meaning that 2/3 of them fall within 1 mpg either side of the true value, and big discrepancies, although rare, are not impossible. Errors of this magnitude (around 2%) are highly plausible given the facts that (a) it is difficult to fill the tank consistently to the brim at the start and end of the assessment period and (b) there could easily be a 5% error in the recorded mileage. Check your speedometer against a satnav if you doubt that.

In the right-hand column of Figure 1 we see the resulting ranking based on a spreadsheet simulating the random errors. The results look fine: drivers A, B and C at the top and X, Y and Z at the bottom, in line with their true performance. But I cheated to get this result: I ran the simulation several times until this outcome occurred.

Figure 2 shows an extract of two other outcomes I got along the way. The top table has driver B promoted from second to first place (benefiting from a 2.3 mpg error), while in the bottom table the same error, combined with bad luck for some of the others, propels driver K into first place from what should have been 11th.

In neither case does the best driver get recognised, and in the top case driver P, actually rather average at 16th, ends up at the bottom thanks to an unlucky but not impossible 7% adverse measurement error.

A league table is pretty daft as a reporting tool. The winners crow about it (deservedly or not) while those at the bottom find excuses or (justifiably)  blame the methodology. As a motivational tool: forget it. When the results are announced, the majority of participants, including those who made a big effort, will see themselves advertised as having failed to get to the top.

Download the simulation to see all this for yourself.